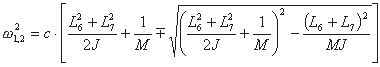Beispiel: Berechnung der Eigenkreisfrequenz
Dieses Beispiel aus der Maschinendynamik befasst sich mit der Ermittlung von
Eigenkreisfrequenzen. Ohne Hintergrundinformation - diese finden Sie im Handbuch - zeigen
wir hier abgekürzt das Vorgehen.
Die Eigenfrequenzen ergeben sich zu:
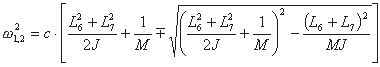
wobei für c gilt:
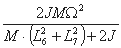
Die Eingabegrößen sind:
- L6 = 220 mm
- L7 = 120 mm
- M = 18 kg (Maschinenmasse)
- J = 0.18 kgm2 (Massenträgheitsmoment)
- n = 1000 min-1 (Nenndrehzahl)
Die Berechnungseinheiten sind [N], [mm] und [s].
Somit geben wir im Konstanteneingabefeld folgende Werte ein:
- L6 = 220 ' [ mm]
- L7 = 120 ' [ mm]
- M = 18/1000 ' [N*s^2/mm]
- J = 0.18E3 ' [N*mm*s^2]
- OMI = 2*PI*1000/60 ' n = 1000 min^(-1)
Die Gleichung schreiben wir für unserere Zwecke um und arbeiten mit Teilgleichungen.
- TC = 2*J*M*OMI^2/(M*(l6^2+L7^2)+2J)
- TG1 = (L6^2+L7^2)/(2J) + 1/M
- TG2 = (L6+L7)^2/(M*J)
Nach diesen Vorbereitungsschritten geben wir im Formeleingabefeld ein:
- f1 = (SQR(TC*(TG1-SQR(TG1^2-TG2))))/(2*PI) ' @
und erhalten nach Betätigung der Return-Taste:
Für die zweite Lösung müssen wir nicht noch mal alles eintippen.
Wir ändern in der, noch im Eingabefeld stehenden, Gleichung:
- "f1" in "f2"
- "-SQR" in "+SQR"
Damit erhalten wir:
- f2 = (SQR(TC*(TG1+SQR(TG1^2-TG2))))/(2*PI) ' @
Wir schließen die Eingabe mit der Return-Taste ab und erhalten die zweite Frequenz zu:
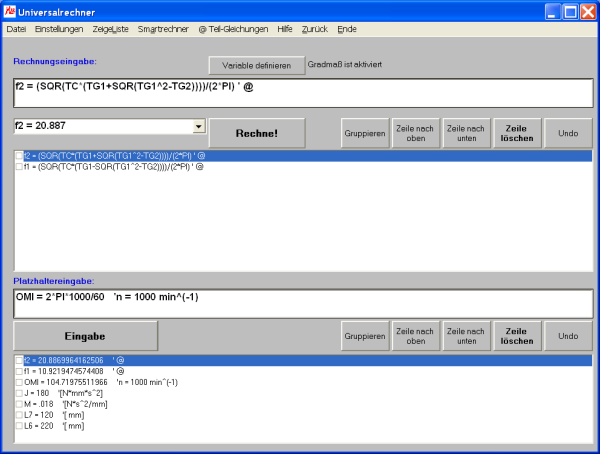
Wir können auch Frequenzänderungen untersuchen. Wenn wir beispielsweise den
Verlauf von f1 nach M erhalten möchten, ist dies ohne weiteres möglich, indem
wir M als Variable definieren. Wir erhalten Wertepaare f1 zu M. Wenn wir diese plotten
möchten, können wir die Tabelle speichern und ins Plotmodul übertragen.
(Zum einfachen Beispiel)
(Zum Beispiel Rissfortschrittsberechnung)
(Zu MAR Cal)
(Zum MAR Plus)
|